It happens that I quite like scientific calculators, and lately I’ve been adding a few to my collection. Several calculators are CAS (“Computer Algebra System”)-capable, meaning they are powerful enough to do symbolic / algebraic processing, and thus are able to understand and manipulate algebraic expressions containing any mix of unknowns, operators and numbers, and simplify, expand, and solve those in a general form. They normally can also do symbolic differentiation and integration, computing the general derivative/integral “function” from a expression first, before you can evaluate them at given points, if desired.
But I’ve always found quite fascinating that some less advanced calculators still offer the possibility of doing numerical integration and differentiation. They don’t know for instance that the derivative function of 3⋅x² is 6⋅x, but they can still tell you that when x = 2 the derivative of 3⋅x² is 12.
Before you ask; I got into this rabbit hole because numerical differentiation and integration are kinda standard features nowadays of any decent calculator. It doesn’t need to be a high end or an expensive calc. In fact, I noticed that even my fx-570MS “entry level” scientific calculator I purchased like 10 years ago can do both operations, while three of my “high end” vintage programmable Casio calculators can’t. As they were “programmable” I think Casio kinda expected users to write their own programs for whatever “advanced” feature they needed. So I started wondering what is the method/algorithm used by current scientific calculators to compute these functions, so I could add the same functionality to my vintage calcs.
Now, I’ll focus on differentiation here because it’s way easier to deconstruct and understand how that works. A post about integration may follow, if this doesn’t turn out to be a massive borefest.
The concept of derivative
So if you go back to the formal definition of a derivative;

You’ll see that it basically attempts to find the “slope” of the function f(x) at a point x by evaluating the expression at x and (x+h) (as you would do with a straight line), and trying to reduce the difference in the X-axis between those two points (h) to a tiny fraction. In fact, it uses the concept of limit to find out where that expression converges when h approaches 0 (It never really gets there though, because the whole expression becomes a division by zero at that point).
This definition allows you to get the derivative as a function (working with x as an unknown), as well as the value it would get at a particular point (using a numerical value “a” for x, representing the point of interest).
You can cheat the definition of limit here for most practical purposes, and simply make the difference h a REALLY small number. With this, even if your calculator can’t tell you the derivative of f(x) as a function, it can still approximate its value at a point x = a, by simply evaluating the original function at two extremely close points around a, and computing the slope between them. In most cases if the points are close enough this approximation will pretty much match the exact value that you’d get by evaluating the actual derivative function at the point of interest.
Now, some calculators will use two points to compute this, others will use 3; Some will let you change the “distance” between the points used to approximate this, some won’t, and we will get to the actual methods used by a few calculators in the following section, together with the drawbacks of each.
Numerical Differentiation
The first method I will cover is the most straightforward one, and in fact, is what I coded before even checking what other calculators were doing. An interesting thing to notice is that if you check your calculator’s manual, chances are that it will tell you the method they use. This way I actually learned that a few calculators used exactly what I did first as a naive approach, while others used a slightly refined method that I’ll cover later.
Method 1: Symmetric Difference Quotient Method
This approach is an almost a verbatim implementation of the formal definition of derivative, but instead of using limits, it uses a “very small value of h”, as discussed earlier, and instead of using x1 = a and x2 = a+h, it puts the point of interest in between, so it will evaluate the function at x1 = (a-h) and x2 = (a+h). Since the point of interest falls in the middle, this method will give you for most cases a really good approximation of the value, if not exactly spot on.
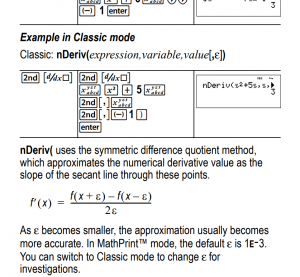
One calculator that uses this method is the Ti 36X Pro. This is an extract from the manual (And it even tells you that they use h=0.001 by default, which turns out to be a really good value for most cases):
There’s one big problem with this approach: We never actually evaluate the function at the point of interest, so this will give you a false reading when the derivative at that point doesn’t exist. Let’s remember that one of the requirements for the derivative of a function to exist, is that the function must be defined at that point. For instance let’s take the function f(x) = 1/x and let’s ask the calculator what’s its derivative at x = 0. The correct answer would be that the derivative at that point doesn’t exist, as the function is not defined for that particular value (1/0 is an illegal operation), but any calculator using this method (like the Ti 36X Pro) will happily tell you otherwise:

Also wrong.
In fact, the reading it will give you corresponds to 1/h²; that is, the inverse of the square of the value used to approximate the derivative. This is because for 1/x when x=0 it will end up calculating the difference between 1/h and -1/h which will result in 2/h… and then will divide that by 2h, giving 1/h². This makes the “f(x) = 1/x test” a really good way for not only checking if your calculator uses this method, but also getting the constant value used for the approximation.
Method 2: Averaging Backward and Forward Differences
This appears to be the favorite method of Casio calculators. You’ll find them in almost every manual of a Casio calcs that can do numerical differentiation (although they will normally simply call it “central difference method” in some manuals, despite that commonly being the name of the approximation method shown before).
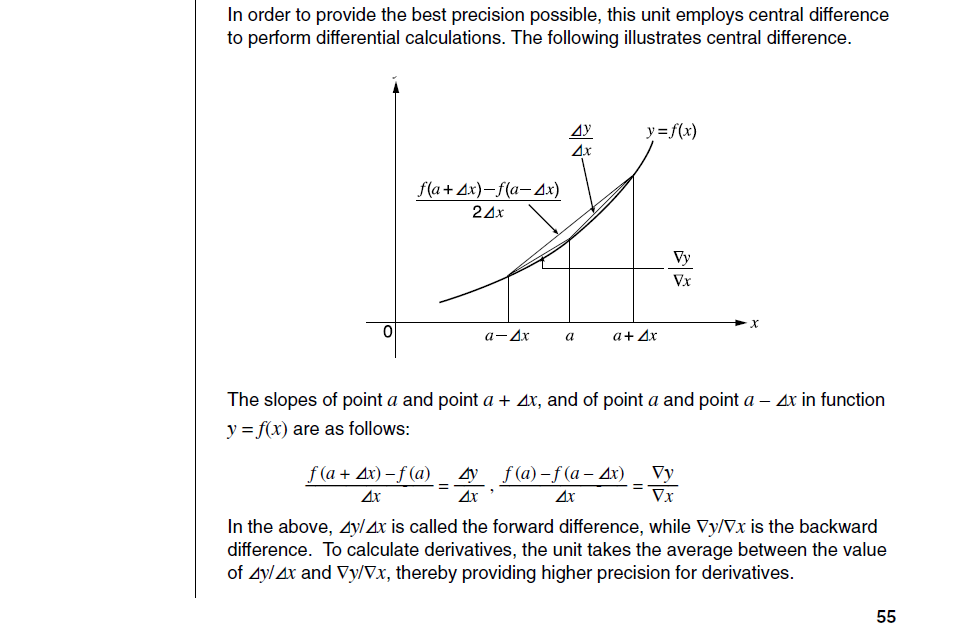
While their use of “Central difference” is kinda confusing, they explicitly tell you that that they compute the forward difference using x=a and x=a+h, and the backward difference (between x=a-h and x=a) and then average the two slopes. This method requires calculating f(x) at the point of interest a, so if the function is not defined at that point, the whole thing will fail and the calculator can tell you that the derivative for that value of x does not exist.
If you take the backward and forward difference and you plug them into a single formula where you average their values, you’ll see that f(a) will cancel out with the other f(a), giving you the exact same formula used for the previous method, so I guess it’s ok for casio to still call this approach the “Central difference method”. The big improvement here though, is that if you do the procedure as they explain it: step by step and using the 3 points initially (despite the middle one being redundant), that will let you determine whether the derivative is valid or not.
With this in mind this seems to be a superior method to the one before, but since it requires a few more intermediate operations to compute essentially the same value, I’d say it’s more prone to rounding errors if the calculator is not smart enough.
As for the internal value of h used by the Casio calculators… they don’t tell you the actual value in the manual (at least not for the CFX series of calculators). They will say however that if you don’t specify a value for h, the calculator will select one for you that works for the expression you are trying to differentiate. Of course this cannot be magic, and I don’t think they are analyzing the actual function you write, so I have a couple of guesses of what they do, and I’ll cover that in the following section.
Common Pitfalls for the unaware
One problem remains common to both methods: Even when the derivative of a function may exist at a given point, the fact that we are using auxiliary points leave us prone to running into a situation where the function is perfectly fine at the point of interest, but not defined at one of our evaluation points. This would again give us a false result.
Let’s take the same f(x) = 1/x function we used before, but let’s try to compute the derivative at x=0.001. We know that the derivative should exist at that point because the function 1/x has no problems for that value of x, so let’s try it.

But also wrong.
At this point it will look like I’m bullying the poor Ti-36X Pro, but I’m not. I really like that calculator, but it’s the only calculator I have with such a naive implementation of numerical differentiation, so please excuse me (I’ll also admit that my initial naive implementation for my calculators suffered from the same exact problems, so I’m not one to talk).
Í’m exploiting the fact that we know beforehand that the calculator uses 0.001 as the value for h. And we know that it will try to calculate f (a-h) at one point. Since we chose a=0.001, that would be 1/ (0.001 – 0.001), which results in a division by zero.
Both methods covered here should be prone to this issue, as long as you can find a point where either f(a+h) or f(a-h) becomes an invalid expression (for their internal choice of h).
Countering this problem
Interestingly enough, I couldn’t make any of my Casio calculators fall for this trick, so you could definitely believe the manual when they say that the calculator is indeed being “smart” and “choosing” a right value of h, appropriate to the function you provided.
Unfortunately for them, there’s a small detail that tells me that this is not as clever or sophisticated as they make us believe it is. These calculators allow you to define yourself the value of h used for the approximation, so in theory by manually setting the value of h to the same I used for a, I should be able to make the calculator fail with the test above. But even my old Casio fx-570MS doesn’t fail with that, and computes the derivative with some degree of accuracy, even when I know for a fact that it has to calculate f(a-h) for the method they use, and that would result in a division by zero with the value I provided for h.
This leads me to believe that they have a “fail-safe” mechanism in place:
They will probably try with an initial value of h (either internal or user-supplied value) and then if it fails, they will modify that value and try again.They’ll probably also have a limit for how many times they will try this before declaring that the function cannot be differentiated at that point, but it’s quite unlikely that you will land in two points where the function is not defined, so even if they only do this once they are most likely protected from most “malicious attacks”.
Now, I also noticed that when I specified h=0.001, my calculator’s answer for the derivative was -999974.6848, which is the exact same value I get if I ask it to use h=0.0001 (a value that shouldn’t cause the expression to be invalid with a=0.001). If I repeat the same test for other values of a and h (with h=a to make the function fail at the lower evaluation point), I will always get the same result if I try with h=a/10. This tells me that the calculator’s “fail-safe” method in case of error, is to divide the previous value of h (either internal or user supplied) by 10 and then attempt to compute the derivative with the new modified value.
Closing Words
The 3-point “Central Difference” method with the fail safe makes for a pretty solid way of doing numerical differentiation, so I’ll probably be modifying my original naive implementation to use this procedure.
I have to admit that I quite enjoyed playing with the calculators to understand what was happening under the hood. These experiments also reinforced my belief that Casio is a pretty strong brand when it comes to calculators. Even my humble fx-570MS responded exceptionally well to my tinkering. Most Casio calculators may look like toys compared to the calculators made by more “serious” brands like Texas Instruments or HP, but their attention to detail and the robustness of their implementations is hard to rival, so they remain among my favorites.